Assessment

What’s in a name? That which we call a rose by any other name would smell as sweet.
— Wm. Shakespeare

Juliet’s famous lament to Romeo was intended to make the obvious but important point that the names we give objects, ideas or indeed ourselves are quite arbitrary, and that these names do not alter the essence of the things themselves. Measurement specialists and test developers have sometimes forgotten this self-evident truth in their laudable zeal to assess human attributes.

Some 30 years ago, the late educational measurement specialist Robert Ebel observed that psychologists do not call a series of word problems, verbal analogies, vocabulary items and quantitative reasoning problems an “Academic Problems Test.” They call it a test of “Mental Ability” or “General Intelligence.” Similarly, a test that asks a series of commonly encountered social and practical problems is not labeled as such, but is called a test of “Practical Judgment.” This type of test is used to support rather tenuous theories of social interaction, since as many have noted, it is a significant leap to conclude that someone who does not answer enough items with the keyed responses is “lacking in practical judgment.”

The reason for the broad labeling of tests is not difficult to discern. The science of psychology, like any other science, requires constructs if it is to progress. In fact, a science progresses precisely in proportion as its constructs are unambiguously defined and measured and their interrelationships clearly specified.

As many have noted, constructs in the social sciences are decidedly more problematic and more difficult to measure than constructs in the physical sciences. The physical constructs of speed, momentum, mass and volume, for example, are unambiguous and, given an agreed upon unit of measure, can be clearly specified. Not so in education and psychology. Nowhere is this more evident than in the development of instruments intended to measure the three related constructs aptitude, ability and achievement. The distinctions among these three concepts are a favorite and long-standing source of disagreement in measurement circles. William Cooley and Paul Lohnes, two educational researchers and policy analysts, argued years ago that the distinction among the three terms is a purely functional one. If a test is used as an indication of past instruction and experience, it is an achievement test. If it is used as a measure of current competence, it is an ability test. If it is used to predict future performance, it is an aptitude test. Yesterday’s achievement is today’s ability and tomorrow’s aptitude. These authors co-mingle items from the Otis-Lennon Mental Ability Test and the Stanford Achievement Test and challenge the reader to distinguish which items are from which test. Their point is well taken. It is virtually impossible to do so.

It is important to note here that Cooley and Lohnes’ perceptive insight regarding the purely functional distinctions among the terms aptitude, ability and achievement was not intended to deny that these are in fact different concepts. Rather, their insight pointed to our inability to construct tests that highlight the differences. In a less enlightened era, we thought that the distinctions among the three concepts were straightforward and that we could devise exercises that would zero in on the difference. That wish was not and is not entirely fanciful. In fact, I would argue that the functional distinction of Cooley and Lohnes is true as far as it goes, but it does not go far enough. There is more to it than that. To ignore or deny the existence of aptitude, for example, would require us to deny the reality of Mozart in music and innumerable prodigies in chess and mathematics.

To take but one example, the verbal reasoning abilities measured by the SAT can and should be distinguished from an achievement test in, say, geography or the French language. In like manner, the quantitative reasoning abilities measured by the SAT-Math are distinguishable from a test that simply assesses one’s declarative knowledge of algebraic rules. The distinction lies in what cognitive scientists call procedural knowledge or, more precisely, the procedural use of declarative knowledge. It is the principal reason that word problems continue to strike fear in the hearts of novice mathematics students.

Unlike many purely academic debates, the distinctions among the concepts of aptitude, ability and achievement have real implications for teaching and learning and for how teachers approach their craft. If a teacher believes that a student’s failure to understand is the result of basic aptitude, then this implies for many a certain withdrawal of additional effort since the problem resides in the student’s basic ability. If, on the other hand, the teacher believes that all children can learn the vast majority of things we want to teach them in school, then a student’s failure to understand a particular concept or principle implies a failure of readiness or motivation on the part of the student, or a failure of pedagogical ingenuity and imagination on the part of the teacher, which in turn implies renewed instructional effort.

Shakespeare was of course right. The names we give objects do not alter the objects themselves, but they may well alter our behavior.

In the background paper for the Carnegie Foundation/Association of American Colleges & Universities project “Integrative Learning: Opportunities to Connect,” Carnegie Senior Scholars Mary Huber and Pat Hutchings summarized the promise and difficulty in fostering and assessing integrative learning within disciplines, across disciplines, between curriculum and co-curriculum, and between academic and professional knowledge and practice. The challenges are familiar and daunting. Despite the near ubiquity of “general education” requirements and the lofty language contained in many college mission statements, the predominant reality is that the college curricular experience is largely fragmented and general education requirements are still viewed by many as something to be “gotten out of the way” before the real business of college begins. The attempts to foster integrative learning through such activities as first-year learning seminars, learning communities, interdisciplinary studies, community-based learning, capstone projects and portfolios tend to be limited to a small number of students and generally isolated from other parts of the curriculum. Moreover, the historically insular character of departments, especially at larger universities, still militates powerfully against coherent efforts at fostering integrative learning in students.

It should therefore not come as a surprise that sustained efforts at assessing integrative learning, and good examples of such assessment, are rare. But existence proofs can be found. In this brief paper, I outline some of the characteristics that a good assessment of integrative learning in its various forms should possess. I lay claim to neither breadth of coverage nor depth of analysis. Rather, what follows is an attempt to specify some desirable properties of a sound assessment of the varied definitions of integrative learning-–from the individual classroom to a summative evaluation of the college experience, and finally to participation in civic life and discourse.

We should note at the outset that there is an understandable reluctance on the part of many faculty to attempt a formal assessment of such concepts as “liberal education” and “integrative learning.” Many feel that such attempts will ultimately trivialize these notions and induce students to adopt a formulaic approach to the assessment. There are good historical reasons for this reluctance. Educational testing is awash with examples of well-motivated and high-minded visions of important educational outcomes that have become polluted by the high-stakes character that the assessment eventually assumes. The SAT in college admissions testing is a classic case in point. Nevertheless the attempt at assessment must be made, for it is axiomatic that if a goal of education is not assessed, then from the student’s perspective it is not valued.

Forms of Assessment
Assessment specialists make a distinction between objectively scored, standardized tests on the one hand, and “performance” tests on the other. Examples of the former include multiple-choice tests, true-false tests, and matching tests. Performance tests, by contrast, are “product- and behavior-based measurements based on settings designed to emulate real life contexts or conditions in which specific knowledge or skills are applied” (Standards for Educational and Psychological Testing, 1999). The virtues and shortcomings of both types of tests are well known. Objective tests can cover an impressively broad area of knowledge, but only in a shallow and relatively impoverished manner. Their hallmark, of course, is their efficiency in scoring. This essay starts with the premise that only performance tests are viable candidates for assessing integrative learning. Scoring such tests is typically labor intensive and may involve considerable time and effort in rubric development and assessor calibration. Short answer assessments are almost by definition inappropriate as measures of integrative learning. No multiple-choice, true-false or matching test can adequately capture students’ ability to integrate what they have learned and display skill in using their knowledge to solve important problems, argue a position, or participate meaningfully in civic life. Equally inappropriate are “well-structured” problems—problems that can be solved quickly, typically have single “correct” answers, and can be easily scored. In fact, the acid test of whether an assessment is inappropriate as a measure of integrative learning is the ease with which it can be scored. In general, the easier the scoring the less likely the assessment will be a viable candidate for gauging integration.

The Centrality of Writing
Before considering some of the elements of a sound system for the assessment of integrative learning, it may be well to discuss briefly the central role of writing in the majority of attempts to gauge integrative learning. Although not all disciplines require writing, and indeed an entire category of artistic endeavor (the performing arts) require virtually no writing, these are the exception. In the vast majority of disciplines, writing about what one knows and can do is the predominant response mode. The requirement to write sometimes introduces a problem known in measurement circles as “construct irrelevant variance.” This concept is best illustrated by example. Imagine a test of quantitative reasoning ability that involves complicated word problems that draw heavily above the student’s ability to decode verbal text. If the difficulty level of the verbal material is sufficiently high, the intended object of measurement (quantitative ability) may be confounded with verbal skills. That is, two persons of comparable quantitative ability would differ in their performance because of differences in the conceptually unrelated construct “verbal ability.”

Construct irrelevant variance is a problem that formal test developers studiously guard against, but it should not distract us here. Full speed ahead. In the assessment of integrative learning, either in the classroom or as a summative senior year experience, the requirement to write about what one knows should not be viewed as a nuisance. In this context of integrative learning, writing ability is not a confounding variable. I believe that one’s writing provides a reliable and valid insight into one’s thinking, which has often been defined as silent speech. It is probably more than that, but I believe the analogy is largely true. If you cannot write clearly and intelligibly (not brilliantly or eloquently, just clearly and intelligibly) about what you know and understand, perhaps it is because you do not really know and you do not really understand.

The Elements of a Sound System for Assessing Integrative Learning
A sound assessment system for a comprehensive performance assessment of integrative learning consists of at minimum the following elements:

(1) The development of a framework and set of assessment specifications; that is, a clear statement of what is to be assessed. This is typically a team effort, and in the present context includes all relevant disciplinary faculty, and in some cases top administrative officials as well.
(2) Development of exercises that reflect the agreed upon assessment specifications. This is no mean task and will require a faculty willing to work to iron out differences of opinion regarding content and emphasis. But it can be done.
(3) A scoring rubric, typically on a 4-point scale, that describes in some detail the elements and characteristics of “inadequate,” “acceptable,” “competent” and “superior” performance.
(4) An assessor (i.e., faculty) training protocol and a procedure for assessor calibration.
(5) A procedure for adjudicating disagreements between assessors.
(6) A quality control mechanism for assuring that assessors remain calibrated and do not “drift” over time.

Although not a formal part of the assessment, one additional element should be a central component of a fair and valid assessment of integrative learning: What is expected of students and the scoring rubric that will be applied to student products? This should be made public and should be widely known and disseminated. There is no need for mystery or secrecy here. In fact, superior as well as inadequate samples of student attempts at integration (possibly with detailed annotations) should be available to students, perhaps on the Internet, so that there is no doubt about what makes some attempts at integration better than others.

No element in the above list should be treated lightly. An apt metaphor for the soundness of an assessment system for integrative learning is the familiar adage, “A chain is only as strong as its weakest link.” An otherwise superior assessment system can be destroyed by, for example, a poor assessor training and calibration. And an outstanding and thorough assessment framework can be rendered useless if scoring is flawed.

Assessing Integration: Notes from the Field
Although the notion of integrative learning may in some sense be a unitary concept, in practice it takes different forms depending upon the level of integration desired. At the level of the academic department in, say, the college of arts and sciences, it is desired that the student be able to integrate the many concepts within a given discipline toward the solution of theoretical or practical problems, or it may be desired to have students integrate their knowledge of two or more disciplines toward the solution of a practical problem. In professional education, the concern is typically that of putting professional knowledge into practice. At the highest institutional level, where “integrative learning” and “liberal education” become virtually indistinguishable, the goal is that students go beyond the integration of formal disciplines to adopt an enlightened disposition toward the world of work, society and civic life. Let us consider specific examples of each of these in turn.

The Assessment of Integrative Learning within a Discipline: An Example from Statistics
In one of the Carnegie Foundation’s Perspectives essays, I cited the example of a gifted instructor who gauged his own teaching by assigning an introductory statistics class a simple question about which of three local grocery stores had the lowest prices. Briefly, teams of three students were each given a week to grapple with this simple question and we had to describe and justify the things we did to arrive at an answer. The same question was repeated at the end of the semester after the class had been introduced to the elegant procedures of statistical inference. As I noted in that essay, the difference in quality between the before and after responses was astonishing.

Although this example was discussed in the context of an argument for pre/post or value added testing in the classroom, it also serves powerfully to illustrate that the assessment of integrative learning within a discipline is within reach of the vast majority of instructors. The grocery store question is simple on its face, but the thought behind it, and the things students must do and know to respond adequately are far from simple. The question has enormous “pulling power”; it evokes a variety of different responses and different approaches to the responses and it provides deep insight into students’ thinking, into how they organize and integrate what they know to sustain a position. The problem requires the student to devise a sampling plan, to determine if statistical weighting is appropriate, to decide upon an appropriate measure of central tendency, to specify a level of statistical significance, to actually carry out the plan, and finally, to analyze and report the results. In short, responses to the question reflect the student’s ability to integrate virtually the sum total of their knowledge of inferential statistical procedures.

Assessing Integrative Learning across Disciplines
Integrative learning across disciplines and its assessment presents special challenges. First, individual professors may not know enough about the various fields to develop assessments and evaluate responses. This implies a team effort and all of the administrative, personality and logistical problems that entails. Integration across disciplines also challenges us as educators to be more deliberate about how we see our own discipline and its connection with other disciplines, with education generally, and with life after formal schooling.

Some professions and majors appear to be natural foils for the development and assessment of cross-disciplinary integration. Engineering, ecology, history, urban planning and social work come immediately to mind, but architecture provides perhaps the archetypal example of a major where integrating across disciplines is not just an ideal; it lies at the very heart of professional practice. Among other things, architects must creatively integrate their knowledge of mathematics, structural engineering, geology, space and human interaction, not to mention their sense of the aesthetic. And although the “table of specifications” for their work may often be quite detailed, the problems they face are fundamentally ill-structured and there is never a single “right” answer. The great span across the Golden Gate could well have been something quite different than the graceful leap we have admired for generations.

In like manner, ecologists must integrate their understanding of various biological, chemical and social phenomena in such a way that the natural environment remains congenial to healthy plant and animal life while at the same time ensuring that economic growth and prosperity are not fatally compromised. Social work majors must integrate their knowledge of developmental, cognitive and social psychology, and marriage and family relations. Learning portfolios and senior capstone projects that require urban planning or ecology majors to analyze a proposed construction project and its environmental impact are excellent examples of assessing integrative learning and thinking toward the solution of practical problems. The requirement of the social work student to write a case study report on a wayward adolescent can be framed in such a way that it provides profound insights into her ability to integrate disciplines relevant to her work.

Assessing Integrative Learning at the Institutional Level
Perhaps nowhere are the measurement challenges more illusive and intractable than in the assessment of integrative learning at the institutional level. Here, integrative learning and liberal education are virtually synonymous concepts.

Although many scholars (beginning with Aristotle and continuing to the present day with Mortimer Adler, Lee Shulman, Robert Hutchins and others) have thought and written widely about the vision of the liberally educated individual, perhaps the most eloquent statement of that vision was crafted over a century ago by William Johnson Cory, the nineteenth century headmaster at Eton. Speaking to an incoming class, he said:

At school you are not engaged so much in acquiring knowledge as in making mental efforts under criticism…A certain amount of knowledge you can indeed with average faculties acquire so as to retain; nor need you regret the hours you spend on much that is forgotten, for the shadow of lost knowledge at least protects you from many illusions. But you go to school not so much for knowledge as for arts and habits; for the habit of attention, for the art of expression, for the art of assuming at a moment’s notice, a new intellectual position, for the art of entering quickly into another person’s thoughts, for the habit of submitting to censure and refutation, for the art of indicating assent or dissent in graduated terms, for the habit of regarding minute points of accuracy, for the art of working out what is possible in a given time; for taste, for discrimination, for mental courage and mental soberness.

Exemplary efforts to assess this vision are hard to find. The long and venerable assessment work at Alverno College perhaps comes closest. An extended discussion of these efforts is beyond the scope of this brief essay, but two publications describing the heroic work at Alverno are well worth the read: Student Assessment-as-Learning at Alverno College (The Alverno College Faculty, 1994) and the award-winning Learning That Lasts: Integrating Learning, Development, and Performance in College and Beyond (M. Mentkowski & Associates, 2000).

An axiom of the measurement and assessment community is “If you would understand a phenomenon, try to measure it.” Attempts to assess whether the undergraduate college experience has equipped students with the disposition to integrate the knowledge and skills they have acquired may well be the most important assessment challenge in higher education today. But initial attempts need not be flawless models of formal assessment; rather, it is important that the attempts be made, for the effort alone will go far in making clear to students one of the important goals of education, and in showing faculty where they have succeeded and where work still needs to be done.

New students to testing are often surprised to find out how modest the relationship is between performance on tests used to predict job performance or college success and actual performance on the job. Normally the correlation is around .30 and rarely is it above .40. What this implies is that approximately 85 percent of the variance in actual performance is not predictable from or explained by test scores. Stated differently, test scores can account for only 15 percent of the variation in individual performance. The lion’s share of the variance in college or job performance must be explained by other factors.

The above summary is, for technical reasons, a bit too pessimistic. Without going into all the gory details, suffice it to say that the actual relationship between tests and actual job performance is higher than the .30 typically observed. There are several reasons for this, but three are particularly important. First, the less than perfect reliability of the test has the effect of lowering the observed correlation between tests and performance. For professionally developed tests, all of which tend to have reliabilities in the range of .90, the effect is relatively small, but it can be accurately estimated.

The second, more important reason has to do with the phenomenon of self-selection. In general, students tend to gravitate toward courses and majors that are better suited to their background and ability. Students who obtain scores between 300 and 400, say on the SAT-Math test, are unlikely to major in mathematics or physics, and are in fact likely to avoid any courses involving substantial mathematical content. At the opposite end, students with high math test scores are more likely to take courses with demanding mathematical content. As a consequence, low scoring students often obtain quite high grade point averages, and students with high test scores often have modest grade point averages. The net result is a lowering of the correlation between test scores and grades.

The final reason is known in the technical literature as the “restriction of range” problem. Other things being equal, the more restricted the range of test scores or grades, the lower the estimated correlation between the two. As one goes up the educational ladder, the range of scholastic ability becomes smaller and smaller. Struggling or disaffected students drop out of high school; many who do graduate never go on to college; many who enroll in college never finish. This restriction is further exacerbated by grade inflation. Again, the net effect is a lowering of the estimated relationship between tests and grades.

When technical adjustments are made for these three factors, the correlation between test scores and performance turns out to be closer to .50 than .30. But even a true correlation as high as .50 means that only approximately 25 percent of the variance in performance is explained by test scores, and 75 percent of the variance must be explained by other factors.

What are some of these other factors that affect performance in college? A candidate list would include at least the following: creativity, emotional and social maturity, time management, good health, efficient study habits and practices, and the absence of personal, family and social problems. There are precious few standardized instruments to measure such attributes. And even if these instruments could be developed, their formal use in college admissions and in employment would no doubt be viewed with skepticism. In the absence of such measures, college admissions officials and employment interviewers rely on a host of other methods such as interviews and letters of recommendation, which in turn have their own problems.

The conclusion here is clear. We cannot materially improve prediction by constructing more reliable tests of the cognitive abilities we already measure since professionally developed tests of human abilities appear to have reached a reliability asymptote (around .90) that has not changed in over 75 years of experience with standardized testing. But even if we could construct tests with reliabilities as high as .95, we would increase the predictive validity only marginally.

If we want to increase our ability to predict who will and who will not succeed in college, on the job or in a profession, we will have to consider more than cognitive tests or tests of content knowledge and look instead to the myriad of other factors that enter into the equation. A complex criterion (college grades, on-the-job performance) requires an equally complex set of predictors. Stated differently, performance that is a function of many abilities and attributes cannot be predicted well by instruments that assess a single construct.

For the greater part of the twentieth century, measurement and assessment specialists employed a simple but surprisingly durable mathematical model to describe and analyze tests used in education, psychology, clinical practice and employment. Briefly, a person’s standing on a test designed to assess a given attribute (call it X) is modeled as a linear, additive function of two more fundamental constructs: a “true” score, T say, and an error component, E:

X = T + E

It is called the Classical Test Theory Model, or the Classical True Score Model, but it is more a model about errors of measurement than true scores. Technically, the true score is defined as the mean score an individual would obtain on either (1) a very large number of “equivalent” or “parallel” tests, or (2) a very large number of administrations of the same test, assuming that each administration is a “new” experience. This definition is purely hypothetical but, as we will see below, it allows us to get a handle on the central concept of an “error” score. The true score is assumed to be stable over some reasonable interval of time. That is, we assume that such human attributes as vocabulary, reading comprehension, practical judgment and introversion are relatively stable traits that do not change dramatically from day to day or week to week. This does not mean that true scores do not change at all. Quite the contrary. A non-French speaking person’s true score on a test of basic French grammar would change dramatically after a year’s study of French.

By contrast, the error component (E) is assumed to be completely random and flip-flops up and down on each measurement occasion. In the hypothetically infinite number of administrations of a test, errors of measurement are assumed to arise from virtually every imaginable source: temporary lapses of attention; lucky guesses on multiple-choice tests; misreading a question; fortuitous (or unfortuitous) sampling of the domain, and so on. The theory assumes that in the long run positive errors and negative errors balance each other out. More precisely, the assumption is that errors of measurement, and therefore the X scores themselves, are normally distributed around individuals’ true scores.

Two fundamental testing concepts are validity and reliability. They are the cornerstone of formal test theory. Validity has traditionally been defined as the extent to which a test measures what it purports to measure. So, for example, a test that claims to measure “quantitative reasoning ability” should measure this ability as “purely” as possible and should not be too contaminated with, say, verbal ability. What this means in practice is that the reading level required by the test should not be so high as to interfere with assessment of the intended construct.

The foregoing definition of validity implies that in a certain sense validity inheres in the test itself. But the modern view is that validity is not strictly a property of the test; a test does not “possess” validity. Rather, validity properly refers to the soundness and defensibility of the interpretations, inferences and uses of test results. It is the interpretations and uses of tests that are either valid or invalid. A test can be valid for one purpose and invalid for another. The use of the SAT-Math test to predict success in college mathematics may constitute a valid use of this test, but using the test to make inferences about the relative quality of high schools would be an invalid use.

Reliability refers to the “repeatability” and stability of the test scores themselves. Note clearly that, unlike validity, the concern here is with the behavior of the numbers themselves, not with their underlying meaning. Specifically, the score a person obtains on an assessment should not change the moment our back is turned. Suppose a group of individuals were administered the same test on two separate occasions. Let us assume that memory per se plays no part in performance on the second administration. (This would be the case, for example, if the test were a measure of proficiency in basic arithmetic operations such as addition and subtraction, manipulation of fractions, long division, and so on. It is unlikely that people would remember each problem and their answers to each problem.) If the test is reliable it should rank order the individuals in essentially the same way on both occasions. If one person obtains a score that places him in the 75th percentile of a given population one week and in the 25th percentile the next week, one would be rightly suspicious of the test’s reliability.

A major factor affecting test reliability is the length of the assessment. An assessment with ten items or exercises will, other things being equal, be less reliable than one with 20 items or exercises. To see why this is so, consider the following thought experiment. Suppose we arranged a golf match between a typical weekend golfer and the phenomenal Tiger Woods. The match (read “test”) will consist of a single, par-3 hole at a suitable golf course. Although unlikely, it is entirely conceivable that the weekend golfer could win this “one item” contest. He or she could get lucky and birdie the hole, or if they are really lucky, get a hole in one. Mr. Woods might well simply par the hole, as he has done countless times in his career. Now suppose that the match consisted not of one hole, but of an entire round of 18 holes. The odds against the weekend golfer winning this longer, more reliable match are enormous. Being lucky once or twice is entirely credible, but being lucky enough to beat Mr. Woods over the entire round taxes credulity. The longer the “test,” the more reliably it reflects the two golfers’ relative ability.

Newcomers to testing theory often confuse validity and reliability; some even use the terms interchangeably. A brief, exaggerated example will illustrate the difference between these two essential testing concepts. We noted above that a reliable test rank orders individuals in essentially the same way on two separate administrations of the test. Now, let us suppose that one were to accept, foolishly, the length of a person’s right index finger as a measure of their vocabulary. To exclude the confounding effects of age, we will restrict our target population to persons 18 years of age and older. This is obviously a hopelessly invalid measure of the construct “vocabulary.” But note that were we to administer our “vocabulary” test on two separate occasions (that is, were we to measure the length of the index fingers of a suitable sample of adults on two separate occasions), the resulting two rank orderings would be virtually identical. We have a highly reliable but utterly invalid test.

The numerical index of reliability is scaled from 0, the total absence of reliability, to 1, perfect reliability. What does zero reliability mean? Consider another thought experiment. Many people believe that there are individuals who are naturally luckier than the rest of us. Suppose we were to test this notion by attempting to rank order people according to their “coin tossing ability.” Our hypothesis is that when instructed to “toss heads,” some individuals can do so consistently more often then others. We instruct 50 randomly chosen individuals to toss a coin 100 times. They are to “attempt to toss as many heads as possible.” We record the number of heads tossed by each individual. The experiment is then repeated and the results are again recorded. It should come as no surprise that the correlation between the first rank order and the second would likely be near zero. The coin-tossing test has essentially zero reliability.

Perfect reliability, on the other hand, implies that both the rank orders and score distributions of a large sample of persons on two administrations of the same test, or on the administrations of equivalent tests, would be identical. The finger test of vocabulary discussed above is an example. In educational and psychological assessment, perfect reliability is hard to come by.

Education is not the filling of a pail, but the lighting of a fire.
—William Butler Yeats

In a Carnegie Perspectives essay, I argued that one way for teachers to gauge their effectiveness is to ask the same carefully crafted questions before and after instruction. The essay sparked a lively debate over what constitutes a teacher’s effect on student learning. One educator, Thorpe Gordon, felt obliged to respond to the criticism that ascribing student learning to an individual teacher during the course of a semester or school year is problematic because students acquire relevant knowledge from many sources external to the class itself, including TV and the Internet. He had this to say:

Is not part of our job to encourage the love of learning and thus the lifelong learning of the topic to which we are presenting the students as their “first course” of a lifelong meal? While teaching environmental scanning in our topic area, I am very pleased if students use their own curiosity to discover other ways of learning and integrating the material, even if that includes the Discovery Channel. Thus, is that also not material that they did not know before the start of the course and the purpose of pre/post testing?

Gordon’s point is on the mark, and it would be unfortunate if readers interpreted my original essay as implying that a teacher’s influence and impact are limited to only that which transpired in the classroom. If the presentation of the subject matter is sufficiently engaging and students are inspired to learn more about the subject from a variety of other sources, well and good. If the class induces in students a heightened sensitivity to incidental information they encounter elsewhere, fine. This is precisely what teachers should strive for, and such learning can rightly be claimed as one of the effects of good instruction. But teacher effects go even beyond this.

When people are asked “Who had the most influence on your life and career?” countless polls and surveys have shown that teachers are second only to parents in the frequency with which they are mentioned. (Aristotle would have reversed the finding. “Those who educate children well,” he wrote, “are more to be honored than parents, for these only gave life, those the art of living well.”)

Two strikingly consistent features of these surveys are that, first, the teachers cited do not come from a single segment of the educational hierarchy, they span the spectrum from elementary school through high school to college and professional school. Second, student testimonials only occasionally center on what went on in class, or the particular knowledge they acquired. For the most part they talk about how the teacher affected their entire disposition toward learning and knowledge. Many even mention a complete shift in their choice of a career.

The U.S. Professor of the Year Program, sponsored jointly by the Carnegie Foundation and The Association of American Colleges and Universities (AACU), has illustrated the latter finding over and over again. The award is given annually to four professors, one each from a community college, a four-year baccalaureate college, a comprehensive university and a doctoral/research university. Nominations must be accompanied by statements of endorsement from colleagues, university administrators and students. (Thanks to Carnegie Senior Scholar Mary Huber, one of the two directors of the program, it has been my good fortune to read many of these statements over the past few years.) The statements from administrators and colleagues are uniformly glowing, but it is those from students that really grab one.

A community college student changed her entire career path (from accounting to writing and liberal arts) as a result of her study with one professor. A student at a doctoral/research university recounts how years after his graduate study his very thinking and approach to his discipline (physics) are still traceable to the mentorship under his major professor. In virtually every student recommendation, the students talked only briefly about what went on in the classroom. Rather, they stressed how their mentors affected their very disposition toward learning and life.

Our understanding of what constitutes good teaching has made enormous strides since the days of classroom observational protocols and behavioral checklists. We now know that a sound assessment of teaching must include, among other things, a thorough examination of teacher assignments, of the student products those assignments evoke, of the quality and usefulness of student feedback, and of how effectively teachers make subject matter content accessible to their students. It is also clear that however refined our assessments of teaching become, they inevitably will tell only part of the story. Henry Adams had it right, “Teachers affect eternity; they can never tell where their influence stops.”

A continuing concern on the part of testing specialists, admissions officers, policy analysts and others is that commercial “coaching” schools for college and graduate school admissions tests, if they are effective in substantially raising students’ scores, could adversely affect the predictive value of such tests in college admissions. It is instructive to examine this concern in some detail.

The coaching debate goes to the heart of several fundamental psychometric questions. What is the nature of the abilities measured by scholastic aptitude tests? Are failures to substantially increase scores through coaching the result of failure in pedagogy or of the inherent difficulty of teaching thinking and reasoning skills? To what extent do score improvements that result from coaching contribute to or detract from test validity?

With respect to the possible adverse affects on predictive validity, three outcomes of coaching are possible. The 2 x 2 table below, a deliberately oversimplified depiction of how college and professional school admissions decisions are actually made, will serve to illustrate these three outcomes. The horizontal axis, representing admission test scores, has been dichotomized into scores below and above the “cut score” for admission. The vertical axis has been dichotomized into successful and unsuccessful performance in school. Applicants in the lower left quadrant and the upper right quadrant represent “correct” admissions decisions. Those in the lower left quadrant (valid rejections) did not achieve scores high enough to be accepted, and, had they been accepted anyway, they would have been unsuccessful. Students in the upper right hand quadrant (valid acceptances) exceeded the cut score on the test and successfully graduated. Applicants in the upper left and lower right quadrants represent incorrect admissions decisions. Those in the upper left quadrant (false rejections) did not achieve scores high enough to be accepted, but had they been accepted, they would have succeeded in college. Those in the lower right quadrant (false acceptances) were accepted in part on the basis of their test scores, but were unsuccessful in college.

One possible effect of coaching is that it might improve both the abilities measured by the tests and the scholastic abilities involved in doing well in college. For the borderline students, coaching in this case (arrow 1) would have the wholly laudatory effect of moving the student from the “valid rejection” category to the “valid acceptance” category. No one could reasonably argue against such an outcome.

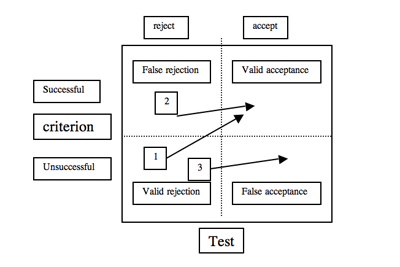
A second possible effect of coaching concerns the student who, because of extreme test anxiety or grossly inefficient test-taking strategies, obtains a score that is not indicative of his or her true academic ability. Coaching in the fundamentals of test taking, such as efficient time allocation and appropriate guessing, might cause the student to be more relaxed and thus improve his or her performance. The test will then be a more veridical reflection of ability. This second case might result in the student moving from the false rejection category to the valid acceptance category (arrow 2) and again this is an unarguably positive outcome.

The third possible outcome of coaching is not so clearly salutary. The coached student moves from the valid rejection category to the false acceptance category (arrow 3). The coached student increases his or her performance on the test, but there is no corresponding increase in the student’s ability to get good grades. Case three is an example of what the late David McClelland derisively called “faking high aptitude.”

Actual research on the extent to which these outcomes occurs is conspicuous by its absence. If the first two results dominate, that simply adds to the validity of the test. If the third turns out to be widespread, then it implies not so much deficiencies in our understanding of scholastic aptitude as serious deficiencies in tests designed to measure that aptitude. In any event, more research is needed on precisely such issues. One way to better understand a phenomenon is to attempt to change it. In so doing, we may come to better understand the nature of expert performance, the optimal conditions under which it progresses, and the instructional environments that foster its development.

In 1989, in a more in-depth treatment of the coaching debate, I concluded with the following statement. I believe it applies with equal force today:

The coaching debate will probably continue unabated for some time to come. One reason for this, of course, is that so long as tests are used in college admissions decisions, students will continue to seek a competitive advantage in gaining admission to the college of their choice. A second more scientifically relevant reason is that recent advances in cognitive psychology have provided some hope in explicating the precise nature of aptitude, how it develops, and how it can be enhanced. This line of research was inspired in part by the controversy surrounding the concepts of aptitude and intelligence and the felt inadequacy of our understanding of both. Green (1981) noted that social and political challenges to a discipline have a way of invigorating it, so that the discipline is likely to prosper. So it is with the coaching debate. Our understanding of human intellectual abilities, as well as out attempts to measure them, is likely to profit from what is both a scientific and a social debate.

Reference
Green, B. F. (1981). A primer of testing. American Psychologist. 10, 1001-1011.
McClelland, D. (1973). Testing for competence rather than intelligence. American Psychologist.

A verbal or “think-aloud” protocol is a transcribed record of a person’s verbalizations of her thinking while attempting to solve a problem or perform a task. In their classic book, Verbal Reports as Data, Ericcson & Simon liken the verbal protocol to observing a dolphin at sea. Because he occasionally goes under water, we see the dolphin only intermittently, not continuously. We must therefore infer his entire path from those times we do see him. A student’s verbalizations during problem solving are surface accounts of her thinking. There are no doubt “under water” periods that we cannot observe and record; but with experience, the analysis of students’ verbalizations while trying to perform a task or solve a problem offers powerful insights into their thinking.

The following problem is an item from a retired form of the SAT-Math test:

If X is an odd number, what is the sum of the next two odd numbers greater than 3X + 1?

(a) 6X + 8
(b) 6X + 6
(c) 6X + 5
(d) 6X + 4
(e) 6X + 3

Less than half of SAT test takers answered this item correctly, and the actual percentage is no doubt smaller since some students guessed the correct alternative. To solve the problem the student must reason as follows:

If X is an odd number, 3X is also odd, and 3X + 1 must be even. The next odd number greater than 3X + 1 is therefore 3X + 2. The next odd number after that is 3X +4. The sum of these two numbers is 6X + 6, so the correct answer is option (b).

The only knowledge required to solve the problem is awareness of the difference between odd and even integers and the rules for simple algebraic addition. Any student who has had an introductory course in Algebra possesses this knowledge, yet more than half could not solve the problem.

Test development companies have data on thousands of such problems from many thousands of students. But for each exercise, the data are restricted to a simple count of the number of students who chose each of the five alternatives. Such data can tell us precious little about how students go about solving such problems or the many misconceptions they carry around in their heads about a given problem’s essential structure. Perhaps more than any other tool in an instructor’s armamentarium, the think-aloud protocol is the prototypical high yield/low stakes assessment.

In a series of studies I conducted some time ago at the University of Pittsburgh, I was interested in why so many students perform well in high school algebra and geometry, but poorly on the SAT-Math test. The performance pattern of high grades/low test scores is an extremely popular one, and the reasons underlying the pattern are many and varied. The 28 students that I studied allowed me to record their verbalizations as they attempted to solve selected math items taken from retired forms of the SAT. All of the students had obtained at least a “B” in both Algebra I and Geometry. Here is the protocol of one student (we will call him R) attempting to solve the above problem. In the transcription, S and E represent the student and the experimenter, respectively.

1. S: If X is an odd number, what is the sum of the next two odd numbers greater than 3X plus 1?
2. (silence)
3. E: What are you thinking about?
4. S: Well, I’m trying to reason out this problem. Uh, ok I was. . . If X is an odd number, what is the sum of the next two odd numbers greater than 3X plus one? So. . . I don’t know, lets see.
5. (long silence)
6. S: I need some help here.
7. E: Ok, hint: If X is an odd number, is 3X even or odd?
8. S: Odd.
9. E: OK. Is 3X plus 1 even or odd?
10. S: Even.
11. E: Now, does that help you?
12. S: Yeah. (long silence)
13. E: Repeat what you know.
14. S: Uh, lets see . . . uh, 3X is odd, 3X plus 1 is . . . even.
15. (long silence)
16. E: What is the next odd number greater than 3X plus 1?
17. S: Three? Put in three for X . . . and add it. So it would be 10?
18. E: Well, we’ve established that 3X plus 1 is even, right?
19. S: Yeah.
20. E: Now, what is the next odd number greater than that?
21. S: Five?
22. E: Well, X can be ANY odd number, 7 say. So if 3X plus 1 is even, what is the next odd number greater than 3X plus 1?
23. S: I don’t know.
24. E: How about 3X plus 2?
25. S: Oh, oh. Aw, man.
26. (mutual laughter)
27. S: I was trying to figure out this 3X . . . I see it now.
28. E: So what’s the next odd number after 3X plus 2?
29. S: 3X plus 3.
30. E: The next ODD number.
31. S: Next ODD number? Oh, oh. You skip that number . . . 3X plus 4. So let’s see…
32. (long silence)
33. E: Read the question.
34. S: (inaudible) Oh, you add. Let’s . . . It’s b. It’s 6X plus 6. Aw, man.

Two points are readily apparent from this protocol. The first is that R could not generate on his own a goal structure for the problem. Yet, when prompted, he provided the correct answers to all relevant subproblems. Second, R does not appear to apprehend the very structure of the problem. This is so despite the fact that the generic character of the correct answer (that is, in the expression 6X + 6, X may be any odd number) can be deduced from the answer set. R tended to represent the problem internally as a problem with a specific rather and a general solution. Hence, in responding (line 13) to my query with a specific number (i.e., 10), he was apparently substituting the specific odd number 3 into the equation 3X + 1. (Even here the student misunderstood the question and simply gave the next integer after 3X, rather than responding with 11, the correct specific answer to the question. This was obviously a simple misunderstanding that was later corrected.) The tendency to respond to the queries with specific numeric answers rather than an algebraic expression in terms of X was common. A sizable plurality of the 28 students gave specific, numeric answers to this same query.

This protocol is also typical in its overall structure. Students were generally unable to generate on their own the series of sub-goals that lead to a correct solution. But they experienced little difficulty in responding correctly to each question posed by the experimenter. The inability to generate an appropriate plan of action and system of sub-goals, coupled with the ability to answer correctly all sub-questions necessary for the correct solution, characterize the majority of protocols for these students.

Compare the above with the following protocol of one of only two students in the sample who obtained “A’s” in both Algebra and Geometry and who scored above 600 on the SAT-Math. The protocols for the above problem produced by these two students were virtually identical.

(Reads question; rereads question)

S: Lets see. If X is odd, then 3X must be . . . odd. And plus 1 must be even. Is that right? Yeah . . . So . . . what is the sum of the next two odd . . . so that’s . . . 3X plus 2 and . . . 3X plus . . . 4. So . . . you add. It’s b, it’s 6X plus 6. (Total time: 52 seconds)

As a general rule, problems like the one above (that is, problems that require relevant, organized knowledge in long-term memory and a set of readily available routines that can be quickly searched during problem solving) presented extreme difficulties for the majority of the students. For many of these students, subproblems requiring simple arithmetic and algebraic routines such as the manipulation of fractions and exponents represented major, time-consuming digressions. In the vernacular of cognitive psychologists, the procedures were never routinized or “automated.” The net effect was that much solution time and in fact much of the students’ working memory were consumed in solving routine intermediate problems, so much so that they often lost track of where they were in the problem.

A careful analysis of these protocols, coupled with observations of algebra classes in the school these students attended, led me to conclude that their difficulties were traceable to how knowledge was initially acquired and stored in long-term memory. The knowledge they acquired about algebra and geometry was largely inert, and was stored in memory as an unconnected and unintegrated list of facts that were largely unavailable during problem solving.

The above insights into student thinking could not have been made from an examination of responses to multiple-choice questions, nor even from responses to open-ended questions where the student is required to “show your work.” For, as any teacher will attest, such instructions often elicit unconnected and undecipherable scribbles that are impossible to follow.

For instructors who have never attempted this powerful assessment technique, the initial foray into verbal protocol analysis may be labor intensive and time-consuming. For students, verbalizing their thoughts during problem solving will be distracting at first, but after several practice problems they quickly catch on and the verbalizations come naturally with fewer and fewer extended silences.

In many circumstances, the verbal protocol may well be the only reliable road into a student’s thinking. It is unquestionably a high yield, low stakes road. I invite teachers to take the drive. They will almost certainly encounter bumps along the way, and a detour or two. But the scenery will intrigue and surprise. Occasionally it will even delight and inspire.

In the introduction to Educating Lawyers: Preparing for the Profession of Law, a book based on the Carnegie Foundation’s study of legal education, Carnegie President Lee Shulman notes that formal preparation for virtually all professions can be characterized by a distinctive set of instructional practices that have come to be called “signature pedagogies.” These are characteristic “forms of instruction that leap to mind when we first think about the preparation of members of particular professions.” The first year of law school, for example, is dominated by the quasi-Socratic “case-dialogue method” where the authoritative instructor in the front of a typically large class engages individual students in a dialogue around judicial opinions in legal cases. These distinctive forms of teaching are not limited to higher education and professional settings. They characterize all levels of education, including the teaching of the very young. If you observed a teacher seated in a circle of about eight children, each holding a book on a small table, and one reading aloud, with the teacher occasionally responding, questioning or correcting, you would be witnessing the distinctive pedagogy of early reading instruction at work.

Why is the study of such pedagogies of interest? Here is Shulman:

[T]hese pedagogical signatures can enlighten us about the personalities, dispositions and cultures of the fields to which they are attached. Moreover, to the extent that they serve as primary means of instruction and socialization for neophytes, they are worthy of our analyses and interpretations, better to understand both their virtues and their flaws.

A similar examination of the distinctive forms of assessment that characterize various educational settings, from primary school through undergraduate education and beyond, would tell us much about the “personalities, dispositions, and cultures” of these settings. As I have argued elsewhere, a discipline’s assessments, the things the discipline requires its apprentices to know and be able to do, reveal in a very direct way what the discipline values, what it deems essential for neophytes to learn.

The question then arises, are there signature assessments that uniquely characterize the evaluation of students across professions, across disciplines and across educational levels? For professions that require formal training at either a university or professional school, the answer seems to be “yes.” More often than not, two distinctive assessments are required, one forming an integral part of professional preparation, the other required for actual practice. In legal education, there is the ubiquitous, three-hour end-of-semester examinations during the first year of law school that for most students determines the very nature and course of their legal careers. This is followed, after graduation, by the equally ubiquitous Multistate Bar Examination.

In teacher education, there is the familiar image of one or more veteran teachers observing from the back of the room a candidate teacher surrounded by a small group of beginning readers or querying a student at the blackboard about long division. Before a license is awarded, candidates in most states must also sit for Praxis I (successor to the National Teacher Examination), a professionally developed standardized test developed by the Educational Testing Service that gauges candidates’ command of basic mathematics and basic English Language Arts. Depending upon their intended teaching field and level, candidate teachers may also be required to take Praxis II, an examination of their command of disciplinary content and their ability to teach that content.

Are there signature assessments that characterize undergraduate education? The multiple-choice test and the open book essay come immediately to mind, but these are not distinctive in the sense that one could distinguish them from any number of non-undergraduate educational contexts. What of liberal education? Is there a signature assessment for liberal education? Inasmuch as a signature pedagogy for liberal education has proven difficult to find [but see Gale (2004) for a cogent argument that the undergraduate seminar may fit the bill] it should not surprise that a signature assessment for liberal education is equally difficult to find.

Were a college or university to attempt such an assessment, it might consider the approach taken by professional test developers. The process begins with a conceptual definition and description of the construct to be assessed. This is followed by the development of a framework and a table of specifications, that is, a specified body of content knowledge crossed with a set of particular skills and proficiencies. These frameworks and specifications are essentially the blueprint for the actual development of the assessment. Depending upon the disciplinary context, the result can be something as straightforward as a multiple-choice test of disciplinary knowledge, or a series of vignettes that the student must analyze in some way, or, as in the case of the National Board for Professional Teaching Standards, a large and complex portfolio that includes examples of a candidate’s lesson plans, samples of student products and candidate feedback, and videotapes with accompanying commentary of the teacher leading both a large group discussion and a small group exercise.

What of a framework and table of specifications for liberal learning? In their background paper for a grant program jointly sponsored by the Carnegie Foundation and the Association of American Colleges and Universities, Huber and Hutchings (2004) explored some of the possibilities and challenges in assessing “integrative learning,” a central component of a liberal education. But a framework and table of specifications for liberal education has not, to my knowledge, been formally undertaken. As Huber and Hutchings note, the assessment challenges are daunting. Not the least of these challenges is collaboration and hopefully consensus among college faculty – a notoriously cantankerous group. The assessment also implies more focus on student self-assessment and a consideration of the kinds of broadening opportunities that colleges and universities make available to students (e.g., community-based learning). The senior capstone report and the “learning portfolio” are leading candidates for such a complex assessment, but they are by no means the final word.

Whether a student intends to practice law, social work or marine biology, the notion persists that her education should not only prepare her for such a life’s work, but should also instill certain habits of mind. It should prepare her to participate as a literate and informed citizen in the life of her community and the larger society.

To be sure, some educators decry the apparent decline in emphasis on liberal education and the view by many faculty and students that “General Studies” are a nuisance, something to be “gotten out of the way.” But the current hegemony of professional education notwithstanding, the liberally educated individual as an educational ideal seems to be an idea that will not die. And an assessment or series of assessments that can capture a coherent vision of liberal education may well be the most important assessment challenge in higher education today.