Is There a Deep Structure to Teaching?
September 13, 2016
Can a teacher certification program be both flexible enough and robust enough that it can be applied with equal fidelity to a teacher in suburban Derrien, Connecticut, in inner-city Detroit, and in rural Mississippi? Can a teacher from small-town Idaho be trained to faithfully apply a scoring rubric to the performance of a teacher in inner-city St. Louis? These were the questions that the National Board for Professional Teaching Standards had to answer if their advanced certification program was ever to get off the ground. As a practical, administrative matter, the National Board needed the flexibility to have assessors rate the performance of teachers regardless of their teaching context. Note that this problem does not come up in many other professions. An assessment of the quality of an appendectomy is essentially the same whether it is performed in Yuma or Chicago. Assessing the quality of a design for a bridge across the Mississippi River is not different in its essential features from assessing the design for a bridge across the Ohio River.
The assessment of teaching, however, presents fundamentally different challenges. First, it is necessary that teachers be assessed in the situations they happen to be in. Attempts to simulate various teaching environments or to have candidates teach a constructed “standard” classroom were rejected as artificial and unrealistic. The National Board could not ask, “How would this teacher perform in a different context, with a different set of students?”
It was essential for the assessors to understand the context in which candidates for certification taught. Assessors had to understand, for example, why a candidate was teaching basic grammar to 16- and 17-year-olds, or why she was teaching fraction to decimal conversion to students whose age suggested they should be taking Algebra II. Certification candidates were therefore instructed to describe in some detail their teaching context: Was the featured class an accelerated one? A remedial one? Were the featured students struggling and seriously behind their age group? What was the SES (Socioeconomic Status) of the school? What was the quality of school resources and support services?
The Board recognized that inevitably some teaching contexts were intensely more difficult than others. But the response to this circumstance was not to throw up their hands in frustration and declare the challenge too difficult to overcome. Rather, the Board’s response was to ask what the teacher did given her teaching context? A guiding principle was that excellence in teaching was not the exclusive province of those who teach in upper middle class communities with energetic, cooperative children who come to school eager to learn. Excellence, it was argued, could be determined on the basis of what teachers do in the circumstances in which they find themselves.
The question actually boils down to whether teaching has a “deep structure” that transcends the very real and important differences in the “surface features” that characterize particular teaching environments. The Board concluded, correctly in my opinion, that teaching indeed has a deep structure and that experienced teachers can be trained to use a flexible yet robust scoring protocol that taps that structure.
The Assessment of “Understanding”
May 29, 2008
Study to remember and you will forget.
Study to understand and you will remember.
—Anonymous
I once sat on the dissertation committee of a graduate student in mathematics education who had examined whether advanced graduate students in math and science education could explain the logic underlying a popular procedure for extracting square roots by hand. Few could explain why the procedure worked. Intrigued by the results, she decided to investigate whether they could explain the logic underlying long division. To her surprise, most in her sample could not. All of the students were adept at division, but few understood why the procedure worked.
In a series of studies at Johns Hopkins University, researchers found that first year physics students could unerringly solve fairly sophisticated problems in classical physics involving moving bodies, but many did not understand the implications of their answers for the behavior of objects in the real world. For example, many could not draw the proper trajectories of objects cut from a swinging pendulum that their equations implied.
What then does it mean to “understand” something—a concept, a scientific principle, an extended rhetorical argument, a procedure or algorithm? What questions might classroom teachers ask of their students, the answers to which would allow a strong inference that the students “understood”? Every educator from kindergarten through graduate and professional school must grapple almost daily with this fundamental question. Do my students really “get it”? Do they genuinely understand the principle I was trying to get across at a level deeper than mere regurgitation? Rather than confront the problem head on, some teachers, perhaps in frustration, sidestep it. Rather then assign projects or construct examinations that probe students’ deep understanding, they require only that students apply the learned procedures to problems highly similar to those discussed in class. Other teachers with the inclination, time and wherewithal often resort to essay tests that invite their students to probe more deeply, but as often as not their students decline the invitation and stay on the surface.
I have thought about issues surrounding the measurement of understanding on and off for years, but have not systematically followed the literature on the topic. On a lark, I conducted three separate Google searches and obtained the following results:
- “nature of understanding” 41,600 hits
- “measurement of understanding” 66,000 hits
- “assessment of understanding” 34,000 hits
Even with the addition of “classroom” to the search, the number of hits exceeded 9,000 for each search. The listings covered the spectrum—from suggestions to elementary school teachers on how to detect “bugs” in children’s understanding of addition and subtraction, to discussions of laboratory studies of brain activity during problem solving, to abstruse philosophical discussions in hermeneutics and epistemology. Clearly, this approach was taking me everywhere, which is to say, nowhere.
Fully aware that I am ignoring much that has been learned, I decided instead to draw upon personal experience—some 30 years in the classroom—to come up with a list of criteria that classroom teachers might use to assess understanding. The list is undoubtedly incomplete, but it is my hope that it will encourage teachers to not only think more carefully about how understanding might be assessed, but also—and perhaps more importantly—encourage them to think more creatively about the kinds of activities they assign their classes. These activities should stimulate students to study for understanding, rather than for mere regurgitation at test time.
The student who understands a principle, rule, procedure or concept should be able to do the following tasks (these are presented in no particular order and their actual difficulties are an empirical question):
Construct problems that illustrate the concept, principle, rule or procedure in question.
As the two anecdotes above illustrate, students may know how to use a procedure or solve specific textbook problems in a domain, but may still not fully understand the principle involved. A more stringent test of understanding would be that they can construct problems themselves that illustrate the principle. In addition to revealing much to instructors about the nature of students’ understanding, problem construction by students can be a powerful learning experience in its own right, for it requires the student to think carefully about such things as problem constraints and data sufficiency.
Identify and, if possible, correct a flawed application of a principle or procedure.
This is basically a check on conceptual and procedural knowledge. If a student truly understands a concept, principle or procedure, she should be able to recognize when it is faithfully and properly applied and when it is not. In the latter case, she should be able to explain and correct the misapplication.
Distinguish between instances and non-instances of a principle; or stated somewhat differently, recognize and explain “problem isomorphs,” that is, problems that differ in their context or surface features, but are illustrations of the same underlying principle.
In a famous and highly cited study by Michelene Chi and her colleagues at the Learning Research and Development Center, novice physics students and professors of physics were each presented with problems typically found in college physics texts and asked to sort or categorized them into groups that “go together” in some sense. They were then asked to explain the basis for their categorization. The basic finding (since replicated in many different disciplines) was that the novice physics students tended to sort problems on the basis of their surface features (e.g., pulley problems, work problems), whereas the experts tended to sort problems on the basis of their “deep structure,” the underlying physical laws that they illustrated (e.g., Newton’s third law of motion, the second law of thermodynamics). This profoundly revealing finding is usually discussed in the context of expert-novice comparisons and in studies of how proficiency develops, but it is also a powerful illustration of deep understanding.
Explain a principle or concept to a naïve audience.
One of the most difficult questions on an examination I took in graduate school was the following: “How would you explain factor analysis to your mother?” That I remember this question over 30 years later is strong testimony to the effect it had on me. I struggled mightily with it. But the question forced me to think about the underlying meaning of factor analysis in ways that had not occurred to me before.
Mathematics educator and researcher, Liping Ma, in her classic exposition Knowing and Teaching Elementary Mathematics (Lawrence Erlbaum, 1999), describes the difficulty some fifth and sixth grade teachers in the United States encounter in explaining fundamental mathematical concepts to their charges. Many of the teachers in her sample, for example, confused division by 1/2 with division by two. The teachers could see on a verbal level that the two were different but they could neither explain the difference nor the numerical implications of that difference. It follows that they could not devise simple story problems and other exercises for fifth and sixth graders that would demonstrate the difference.
To be sure, students may well understand a principle, procedure or concept without being able to do all of the above. But a student who can do none of the above almost certainly does not understand, and students who can perform all of the above tasks flawlessly almost certainly do understand.
One point appears certain: relying solely on the problems at the end of each chapter in text books, many of which have been written by harried and stressed-out graduate students, will not assure that our students understand the concepts we wish to teach them. The extended essay has been the solution of choice for many instructors whose teaching load and class size permit such a luxury. But less labor intensive ways of assessing understanding are sorely needed.
A perpetually vexing problem in American education is the substantially lower mean levels of achievement in virtually all academic subjects by African American, Hispanic, and poor students. The problem is evident from varied but consistent indices: lower grades, lower performance on state-mandated standardized tests, substantially higher drop out rates, and lower average performance on college admissions tests.
Historically, two schools of thought have dominated the debate over how best to gauge whether individual schools are doing a good job of educating these students. One might be called the “valued-added” school and the other the “final status” school. Advocates of the value-added criterion maintain that the only reasonable and fair standard for assessing school effectiveness is how effectively schools educate students, given their entering level of achievement. The argument is that it is simply unreasonable to expect schools in the nation’s large urban areas to produce the same levels of achievement as well-funded suburban schools. In their paper in ERS Spectrum (Spring, 2005), entitled “The Perfect Storm in Urban Schools: Student, Teacher, and Principal Transience,” researchers Hampton and Purcell of Cleveland State University describe in painful detail the dimensions of the problems faced by the vast majority of the nation’s urban schools. The picture they describe is not pretty. Against a community backdrop of linguistic diversity, broken-homes, poverty, joblessness, and despair is a confluence of transiencies—a transience of students, a transience of teachers, a transience of principals, and, they might well have added, a transience of superintendents. All combine to form a “perfect storm” that could not have been purposefully scripted better to produce lasting and pervasive failure. No wonder the modest “value-added” approach to assessing school quality has such widespread appeal.
The alternative view is that a goal of modest year-to-year growth for students who are seriously behind their peers is both defeatist and demeaning. Clinical mental retardation excepted, all students can learn and can achieve at high levels, and accepting anything less than excellence is to admit defeat. Moreover, the value-added approach to assessing school effectiveness carries for many the odious implication that such limited achievement is all that these students are capable of.
The argument of the “final status” advocates gains considerable credibility when they point to “existence proofs,” inner-city schools whose students’ performance on any number of achievement measures is comparable to those of the best schools in the metropolitan area. The R. L. Vann School in the poverty-stricken “Hill District” of Pittsburgh, Pennsylvania, with a 99% African American student body, is a case in point. Although I have not followed its progress in recent years, throughout the 1970’s and 80’s, the school consistently performed on a par with the best schools in the area on any number of standardized achievement tests in math and English Language Arts. For readers with a statistical bent, the situation is dramatically illustrated when the Pittsburgh school medians on standardized tests are plotted against school SES (as indexed by “percent free lunch”). On first blush, the scatter plot of points appears to be a misprint, with the Vann School appearing as an outlier in the extreme upper left hand corner of the swarm of points. The school is in the top quarter in achievement and the bottom quarter in SES.
The controversial and politically explosive No Child Left Behind Act (NCLB) has placed both the Achievement Gap and the “value added vs. final status” controversy in stark relief. NCLB requires among other things that states specify for their schools “adequate yearly progress” toward reducing the achievement gap. The legislation has reawakened a host of old and difficult questions: What will we accept as “adequate yearly progress?” What role should standardized tests play in monitoring student achievement and in evaluating teacher and principal effectiveness? What is the best way to gauge “school effectiveness?” Put more starkly, What do we mean by a “successful” or “effective” school, and what do we mean by a “failing” or “unsuccessful” one? These questions take on enormous political, social and even moral overtones when they are applied equally to an under-funded urban school populated primarily by poor and minority children, on the one hand, and to a well-funded suburban school populated by middle and upper-class majority students, on the other.
The most contentious provisions of the bill are the series of sanctions for continued failure to meet the specified adequate yearly progress. These cover the spectrum from developing and implementing a plan for improvement, to allowing the affected students to change schools, to turning the school over to the state or a private, for-profit agency with a proven record of success. Several states have sued in federal court arguing that such sanctions without federally appropriated money to finance needed improvements are unconstitutional.
In such a climate, where the very motives of each side in the debate are often impugned, it is easy to lose sight of what should be our common goal. We may disagree about means and methods, but we should be united in our commitment as educators and citizens to the ultimate end in view, exemplified in the words of no less a thinker than John Dewey. A century ago he wrote, “What the best and wisest parent wants for his own child, that must the community want for all its children. Any other ideal for our schools is narrow and unlovely; acted upon it destroys our democracy.”
References
Dewey, J. (1907). The School and Society. Chicago: University of Chicago Press (1907).
Hampton, F., & Purcell, T. (2005). “The Perfect Storm in Urban Schools: Student, Teacher, and Principal Transience.” ERS Spectrum, 23(2), 12-22.
1 row in set (0.00 sec)
Aptitude, Ability, and Achievement
October 25, 2007
What’s in a name? That which we call a rose by any other name would smell as sweet.
— Wm. Shakespeare
Juliet’s famous lament to Romeo was intended to make the obvious but important point that the names we give objects, ideas or indeed ourselves are quite arbitrary, and that these names do not alter the essence of the things themselves. Measurement specialists and test developers have sometimes forgotten this self-evident truth in their laudable zeal to assess human attributes.
Some 30 years ago, the late educational measurement specialist Robert Ebel observed that psychologists do not call a series of word problems, verbal analogies, vocabulary items and quantitative reasoning problems an “Academic Problems Test.” They call it a test of “Mental Ability” or “General Intelligence.” Similarly, a test that asks a series of commonly encountered social and practical problems is not labeled as such, but is called a test of “Practical Judgment.” This type of test is used to support rather tenuous theories of social interaction, since as many have noted, it is a significant leap to conclude that someone who does not answer enough items with the keyed responses is “lacking in practical judgment.”
The reason for the broad labeling of tests is not difficult to discern. The science of psychology, like any other science, requires constructs if it is to progress. In fact, a science progresses precisely in proportion as its constructs are unambiguously defined and measured and their interrelationships clearly specified.
As many have noted, constructs in the social sciences are decidedly more problematic and more difficult to measure than constructs in the physical sciences. The physical constructs of speed, momentum, mass and volume, for example, are unambiguous and, given an agreed upon unit of measure, can be clearly specified. Not so in education and psychology. Nowhere is this more evident than in the development of instruments intended to measure the three related constructs aptitude, ability and achievement. The distinctions among these three concepts are a favorite and long-standing source of disagreement in measurement circles. William Cooley and Paul Lohnes, two educational researchers and policy analysts, argued years ago that the distinction among the three terms is a purely functional one. If a test is used as an indication of past instruction and experience, it is an achievement test. If it is used as a measure of current competence, it is an ability test. If it is used to predict future performance, it is an aptitude test. Yesterday’s achievement is today’s ability and tomorrow’s aptitude. These authors co-mingle items from the Otis-Lennon Mental Ability Test and the Stanford Achievement Test and challenge the reader to distinguish which items are from which test. Their point is well taken. It is virtually impossible to do so.
It is important to note here that Cooley and Lohnes’ perceptive insight regarding the purely functional distinctions among the terms aptitude, ability and achievement was not intended to deny that these are in fact different concepts. Rather, their insight pointed to our inability to construct tests that highlight the differences. In a less enlightened era, we thought that the distinctions among the three concepts were straightforward and that we could devise exercises that would zero in on the difference. That wish was not and is not entirely fanciful. In fact, I would argue that the functional distinction of Cooley and Lohnes is true as far as it goes, but it does not go far enough. There is more to it than that. To ignore or deny the existence of aptitude, for example, would require us to deny the reality of Mozart in music and innumerable prodigies in chess and mathematics.
To take but one example, the verbal reasoning abilities measured by the SAT can and should be distinguished from an achievement test in, say, geography or the French language. In like manner, the quantitative reasoning abilities measured by the SAT-Math are distinguishable from a test that simply assesses one’s declarative knowledge of algebraic rules. The distinction lies in what cognitive scientists call procedural knowledge or, more precisely, the procedural use of declarative knowledge. It is the principal reason that word problems continue to strike fear in the hearts of novice mathematics students.
Unlike many purely academic debates, the distinctions among the concepts of aptitude, ability and achievement have real implications for teaching and learning and for how teachers approach their craft. If a teacher believes that a student’s failure to understand is the result of basic aptitude, then this implies for many a certain withdrawal of additional effort since the problem resides in the student’s basic ability. If, on the other hand, the teacher believes that all children can learn the vast majority of things we want to teach them in school, then a student’s failure to understand a particular concept or principle implies a failure of readiness or motivation on the part of the student, or a failure of pedagogical ingenuity and imagination on the part of the teacher, which in turn implies renewed instructional effort.
Shakespeare was of course right. The names we give objects do not alter the objects themselves, but they may well alter our behavior.
Toward a Framework for the Assessment of Integrative Learning
October 25, 2007
In the background paper for the Carnegie Foundation/Association of American Colleges & Universities project “Integrative Learning: Opportunities to Connect,” Carnegie Senior Scholars Mary Huber and Pat Hutchings summarized the promise and difficulty in fostering and assessing integrative learning within disciplines, across disciplines, between curriculum and co-curriculum, and between academic and professional knowledge and practice. The challenges are familiar and daunting. Despite the near ubiquity of “general education” requirements and the lofty language contained in many college mission statements, the predominant reality is that the college curricular experience is largely fragmented and general education requirements are still viewed by many as something to be “gotten out of the way” before the real business of college begins. The attempts to foster integrative learning through such activities as first-year learning seminars, learning communities, interdisciplinary studies, community-based learning, capstone projects and portfolios tend to be limited to a small number of students and generally isolated from other parts of the curriculum. Moreover, the historically insular character of departments, especially at larger universities, still militates powerfully against coherent efforts at fostering integrative learning in students.
It should therefore not come as a surprise that sustained efforts at assessing integrative learning, and good examples of such assessment, are rare. But existence proofs can be found. In this brief paper, I outline some of the characteristics that a good assessment of integrative learning in its various forms should possess. I lay claim to neither breadth of coverage nor depth of analysis. Rather, what follows is an attempt to specify some desirable properties of a sound assessment of the varied definitions of integrative learning-–from the individual classroom to a summative evaluation of the college experience, and finally to participation in civic life and discourse.
We should note at the outset that there is an understandable reluctance on the part of many faculty to attempt a formal assessment of such concepts as “liberal education” and “integrative learning.” Many feel that such attempts will ultimately trivialize these notions and induce students to adopt a formulaic approach to the assessment. There are good historical reasons for this reluctance. Educational testing is awash with examples of well-motivated and high-minded visions of important educational outcomes that have become polluted by the high-stakes character that the assessment eventually assumes. The SAT in college admissions testing is a classic case in point. Nevertheless the attempt at assessment must be made, for it is axiomatic that if a goal of education is not assessed, then from the student’s perspective it is not valued.
Forms of Assessment
Assessment specialists make a distinction between objectively scored, standardized tests on the one hand, and “performance” tests on the other. Examples of the former include multiple-choice tests, true-false tests, and matching tests. Performance tests, by contrast, are “product- and behavior-based measurements based on settings designed to emulate real life contexts or conditions in which specific knowledge or skills are applied” (Standards for Educational and Psychological Testing, 1999). The virtues and shortcomings of both types of tests are well known. Objective tests can cover an impressively broad area of knowledge, but only in a shallow and relatively impoverished manner. Their hallmark, of course, is their efficiency in scoring. This essay starts with the premise that only performance tests are viable candidates for assessing integrative learning. Scoring such tests is typically labor intensive and may involve considerable time and effort in rubric development and assessor calibration. Short answer assessments are almost by definition inappropriate as measures of integrative learning. No multiple-choice, true-false or matching test can adequately capture students’ ability to integrate what they have learned and display skill in using their knowledge to solve important problems, argue a position, or participate meaningfully in civic life. Equally inappropriate are “well-structured” problems—problems that can be solved quickly, typically have single “correct” answers, and can be easily scored. In fact, the acid test of whether an assessment is inappropriate as a measure of integrative learning is the ease with which it can be scored. In general, the easier the scoring the less likely the assessment will be a viable candidate for gauging integration.
The Centrality of Writing
Before considering some of the elements of a sound system for the assessment of integrative learning, it may be well to discuss briefly the central role of writing in the majority of attempts to gauge integrative learning. Although not all disciplines require writing, and indeed an entire category of artistic endeavor (the performing arts) require virtually no writing, these are the exception. In the vast majority of disciplines, writing about what one knows and can do is the predominant response mode. The requirement to write sometimes introduces a problem known in measurement circles as “construct irrelevant variance.” This concept is best illustrated by example. Imagine a test of quantitative reasoning ability that involves complicated word problems that draw heavily above the student’s ability to decode verbal text. If the difficulty level of the verbal material is sufficiently high, the intended object of measurement (quantitative ability) may be confounded with verbal skills. That is, two persons of comparable quantitative ability would differ in their performance because of differences in the conceptually unrelated construct “verbal ability.”
Construct irrelevant variance is a problem that formal test developers studiously guard against, but it should not distract us here. Full speed ahead. In the assessment of integrative learning, either in the classroom or as a summative senior year experience, the requirement to write about what one knows should not be viewed as a nuisance. In this context of integrative learning, writing ability is not a confounding variable. I believe that one’s writing provides a reliable and valid insight into one’s thinking, which has often been defined as silent speech. It is probably more than that, but I believe the analogy is largely true. If you cannot write clearly and intelligibly (not brilliantly or eloquently, just clearly and intelligibly) about what you know and understand, perhaps it is because you do not really know and you do not really understand.
The Elements of a Sound System for Assessing Integrative Learning
A sound assessment system for a comprehensive performance assessment of integrative learning consists of at minimum the following elements:
(1) The development of a framework and set of assessment specifications; that is, a clear statement of what is to be assessed. This is typically a team effort, and in the present context includes all relevant disciplinary faculty, and in some cases top administrative officials as well.
(2) Development of exercises that reflect the agreed upon assessment specifications. This is no mean task and will require a faculty willing to work to iron out differences of opinion regarding content and emphasis. But it can be done.
(3) A scoring rubric, typically on a 4-point scale, that describes in some detail the elements and characteristics of “inadequate,” “acceptable,” “competent” and “superior” performance.
(4) An assessor (i.e., faculty) training protocol and a procedure for assessor calibration.
(5) A procedure for adjudicating disagreements between assessors.
(6) A quality control mechanism for assuring that assessors remain calibrated and do not “drift” over time.
Although not a formal part of the assessment, one additional element should be a central component of a fair and valid assessment of integrative learning: What is expected of students and the scoring rubric that will be applied to student products? This should be made public and should be widely known and disseminated. There is no need for mystery or secrecy here. In fact, superior as well as inadequate samples of student attempts at integration (possibly with detailed annotations) should be available to students, perhaps on the Internet, so that there is no doubt about what makes some attempts at integration better than others.
No element in the above list should be treated lightly. An apt metaphor for the soundness of an assessment system for integrative learning is the familiar adage, “A chain is only as strong as its weakest link.” An otherwise superior assessment system can be destroyed by, for example, a poor assessor training and calibration. And an outstanding and thorough assessment framework can be rendered useless if scoring is flawed.
Assessing Integration: Notes from the Field
Although the notion of integrative learning may in some sense be a unitary concept, in practice it takes different forms depending upon the level of integration desired. At the level of the academic department in, say, the college of arts and sciences, it is desired that the student be able to integrate the many concepts within a given discipline toward the solution of theoretical or practical problems, or it may be desired to have students integrate their knowledge of two or more disciplines toward the solution of a practical problem. In professional education, the concern is typically that of putting professional knowledge into practice. At the highest institutional level, where “integrative learning” and “liberal education” become virtually indistinguishable, the goal is that students go beyond the integration of formal disciplines to adopt an enlightened disposition toward the world of work, society and civic life. Let us consider specific examples of each of these in turn.
The Assessment of Integrative Learning within a Discipline: An Example from Statistics
In one of the Carnegie Foundation’s Perspectives essays, I cited the example of a gifted instructor who gauged his own teaching by assigning an introductory statistics class a simple question about which of three local grocery stores had the lowest prices. Briefly, teams of three students were each given a week to grapple with this simple question and we had to describe and justify the things we did to arrive at an answer. The same question was repeated at the end of the semester after the class had been introduced to the elegant procedures of statistical inference. As I noted in that essay, the difference in quality between the before and after responses was astonishing.
Although this example was discussed in the context of an argument for pre/post or value added testing in the classroom, it also serves powerfully to illustrate that the assessment of integrative learning within a discipline is within reach of the vast majority of instructors. The grocery store question is simple on its face, but the thought behind it, and the things students must do and know to respond adequately are far from simple. The question has enormous “pulling power”; it evokes a variety of different responses and different approaches to the responses and it provides deep insight into students’ thinking, into how they organize and integrate what they know to sustain a position. The problem requires the student to devise a sampling plan, to determine if statistical weighting is appropriate, to decide upon an appropriate measure of central tendency, to specify a level of statistical significance, to actually carry out the plan, and finally, to analyze and report the results. In short, responses to the question reflect the student’s ability to integrate virtually the sum total of their knowledge of inferential statistical procedures.
Assessing Integrative Learning across Disciplines
Integrative learning across disciplines and its assessment presents special challenges. First, individual professors may not know enough about the various fields to develop assessments and evaluate responses. This implies a team effort and all of the administrative, personality and logistical problems that entails. Integration across disciplines also challenges us as educators to be more deliberate about how we see our own discipline and its connection with other disciplines, with education generally, and with life after formal schooling.
Some professions and majors appear to be natural foils for the development and assessment of cross-disciplinary integration. Engineering, ecology, history, urban planning and social work come immediately to mind, but architecture provides perhaps the archetypal example of a major where integrating across disciplines is not just an ideal; it lies at the very heart of professional practice. Among other things, architects must creatively integrate their knowledge of mathematics, structural engineering, geology, space and human interaction, not to mention their sense of the aesthetic. And although the “table of specifications” for their work may often be quite detailed, the problems they face are fundamentally ill-structured and there is never a single “right” answer. The great span across the Golden Gate could well have been something quite different than the graceful leap we have admired for generations.
In like manner, ecologists must integrate their understanding of various biological, chemical and social phenomena in such a way that the natural environment remains congenial to healthy plant and animal life while at the same time ensuring that economic growth and prosperity are not fatally compromised. Social work majors must integrate their knowledge of developmental, cognitive and social psychology, and marriage and family relations. Learning portfolios and senior capstone projects that require urban planning or ecology majors to analyze a proposed construction project and its environmental impact are excellent examples of assessing integrative learning and thinking toward the solution of practical problems. The requirement of the social work student to write a case study report on a wayward adolescent can be framed in such a way that it provides profound insights into her ability to integrate disciplines relevant to her work.
Assessing Integrative Learning at the Institutional Level
Perhaps nowhere are the measurement challenges more illusive and intractable than in the assessment of integrative learning at the institutional level. Here, integrative learning and liberal education are virtually synonymous concepts.
Although many scholars (beginning with Aristotle and continuing to the present day with Mortimer Adler, Lee Shulman, Robert Hutchins and others) have thought and written widely about the vision of the liberally educated individual, perhaps the most eloquent statement of that vision was crafted over a century ago by William Johnson Cory, the nineteenth century headmaster at Eton. Speaking to an incoming class, he said:
At school you are not engaged so much in acquiring knowledge as in making mental efforts under criticism…A certain amount of knowledge you can indeed with average faculties acquire so as to retain; nor need you regret the hours you spend on much that is forgotten, for the shadow of lost knowledge at least protects you from many illusions. But you go to school not so much for knowledge as for arts and habits; for the habit of attention, for the art of expression, for the art of assuming at a moment’s notice, a new intellectual position, for the art of entering quickly into another person’s thoughts, for the habit of submitting to censure and refutation, for the art of indicating assent or dissent in graduated terms, for the habit of regarding minute points of accuracy, for the art of working out what is possible in a given time; for taste, for discrimination, for mental courage and mental soberness.
Exemplary efforts to assess this vision are hard to find. The long and venerable assessment work at Alverno College perhaps comes closest. An extended discussion of these efforts is beyond the scope of this brief essay, but two publications describing the heroic work at Alverno are well worth the read: Student Assessment-as-Learning at Alverno College (The Alverno College Faculty, 1994) and the award-winning Learning That Lasts: Integrating Learning, Development, and Performance in College and Beyond (M. Mentkowski & Associates, 2000).
An axiom of the measurement and assessment community is “If you would understand a phenomenon, try to measure it.” Attempts to assess whether the undergraduate college experience has equipped students with the disposition to integrate the knowledge and skills they have acquired may well be the most important assessment challenge in higher education today. But initial attempts need not be flawless models of formal assessment; rather, it is important that the attempts be made, for the effort alone will go far in making clear to students one of the important goals of education, and in showing faculty where they have succeeded and where work still needs to be done.
Predicting Complex Performance
October 25, 2007
New students to testing are often surprised to find out how modest the relationship is between performance on tests used to predict job performance or college success and actual performance on the job. Normally the correlation is around .30 and rarely is it above .40. What this implies is that approximately 85 percent of the variance in actual performance is not predictable from or explained by test scores. Stated differently, test scores can account for only 15 percent of the variation in individual performance. The lion’s share of the variance in college or job performance must be explained by other factors.
The above summary is, for technical reasons, a bit too pessimistic. Without going into all the gory details, suffice it to say that the actual relationship between tests and actual job performance is higher than the .30 typically observed. There are several reasons for this, but three are particularly important. First, the less than perfect reliability of the test has the effect of lowering the observed correlation between tests and performance. For professionally developed tests, all of which tend to have reliabilities in the range of .90, the effect is relatively small, but it can be accurately estimated.
The second, more important reason has to do with the phenomenon of self-selection. In general, students tend to gravitate toward courses and majors that are better suited to their background and ability. Students who obtain scores between 300 and 400, say on the SAT-Math test, are unlikely to major in mathematics or physics, and are in fact likely to avoid any courses involving substantial mathematical content. At the opposite end, students with high math test scores are more likely to take courses with demanding mathematical content. As a consequence, low scoring students often obtain quite high grade point averages, and students with high test scores often have modest grade point averages. The net result is a lowering of the correlation between test scores and grades.
The final reason is known in the technical literature as the “restriction of range” problem. Other things being equal, the more restricted the range of test scores or grades, the lower the estimated correlation between the two. As one goes up the educational ladder, the range of scholastic ability becomes smaller and smaller. Struggling or disaffected students drop out of high school; many who do graduate never go on to college; many who enroll in college never finish. This restriction is further exacerbated by grade inflation. Again, the net effect is a lowering of the estimated relationship between tests and grades.
When technical adjustments are made for these three factors, the correlation between test scores and performance turns out to be closer to .50 than .30. But even a true correlation as high as .50 means that only approximately 25 percent of the variance in performance is explained by test scores, and 75 percent of the variance must be explained by other factors.
What are some of these other factors that affect performance in college? A candidate list would include at least the following: creativity, emotional and social maturity, time management, good health, efficient study habits and practices, and the absence of personal, family and social problems. There are precious few standardized instruments to measure such attributes. And even if these instruments could be developed, their formal use in college admissions and in employment would no doubt be viewed with skepticism. In the absence of such measures, college admissions officials and employment interviewers rely on a host of other methods such as interviews and letters of recommendation, which in turn have their own problems.
The conclusion here is clear. We cannot materially improve prediction by constructing more reliable tests of the cognitive abilities we already measure since professionally developed tests of human abilities appear to have reached a reliability asymptote (around .90) that has not changed in over 75 years of experience with standardized testing. But even if we could construct tests with reliabilities as high as .95, we would increase the predictive validity only marginally.
If we want to increase our ability to predict who will and who will not succeed in college, on the job or in a profession, we will have to consider more than cognitive tests or tests of content knowledge and look instead to the myriad of other factors that enter into the equation. A complex criterion (college grades, on-the-job performance) requires an equally complex set of predictors. Stated differently, performance that is a function of many abilities and attributes cannot be predicted well by instruments that assess a single construct.
A Little Test Theory
October 25, 2007
For the greater part of the twentieth century, measurement and assessment specialists employed a simple but surprisingly durable mathematical model to describe and analyze tests used in education, psychology, clinical practice and employment. Briefly, a person’s standing on a test designed to assess a given attribute (call it X) is modeled as a linear, additive function of two more fundamental constructs: a “true” score, T say, and an error component, E:
X = T + E
It is called the Classical Test Theory Model, or the Classical True Score Model, but it is more a model about errors of measurement than true scores. Technically, the true score is defined as the mean score an individual would obtain on either (1) a very large number of “equivalent” or “parallel” tests, or (2) a very large number of administrations of the same test, assuming that each administration is a “new” experience. This definition is purely hypothetical but, as we will see below, it allows us to get a handle on the central concept of an “error” score. The true score is assumed to be stable over some reasonable interval of time. That is, we assume that such human attributes as vocabulary, reading comprehension, practical judgment and introversion are relatively stable traits that do not change dramatically from day to day or week to week. This does not mean that true scores do not change at all. Quite the contrary. A non-French speaking person’s true score on a test of basic French grammar would change dramatically after a year’s study of French.
By contrast, the error component (E) is assumed to be completely random and flip-flops up and down on each measurement occasion. In the hypothetically infinite number of administrations of a test, errors of measurement are assumed to arise from virtually every imaginable source: temporary lapses of attention; lucky guesses on multiple-choice tests; misreading a question; fortuitous (or unfortuitous) sampling of the domain, and so on. The theory assumes that in the long run positive errors and negative errors balance each other out. More precisely, the assumption is that errors of measurement, and therefore the X scores themselves, are normally distributed around individuals’ true scores.
Two fundamental testing concepts are validity and reliability. They are the cornerstone of formal test theory. Validity has traditionally been defined as the extent to which a test measures what it purports to measure. So, for example, a test that claims to measure “quantitative reasoning ability” should measure this ability as “purely” as possible and should not be too contaminated with, say, verbal ability. What this means in practice is that the reading level required by the test should not be so high as to interfere with assessment of the intended construct.
The foregoing definition of validity implies that in a certain sense validity inheres in the test itself. But the modern view is that validity is not strictly a property of the test; a test does not “possess” validity. Rather, validity properly refers to the soundness and defensibility of the interpretations, inferences and uses of test results. It is the interpretations and uses of tests that are either valid or invalid. A test can be valid for one purpose and invalid for another. The use of the SAT-Math test to predict success in college mathematics may constitute a valid use of this test, but using the test to make inferences about the relative quality of high schools would be an invalid use.
Reliability refers to the “repeatability” and stability of the test scores themselves. Note clearly that, unlike validity, the concern here is with the behavior of the numbers themselves, not with their underlying meaning. Specifically, the score a person obtains on an assessment should not change the moment our back is turned. Suppose a group of individuals were administered the same test on two separate occasions. Let us assume that memory per se plays no part in performance on the second administration. (This would be the case, for example, if the test were a measure of proficiency in basic arithmetic operations such as addition and subtraction, manipulation of fractions, long division, and so on. It is unlikely that people would remember each problem and their answers to each problem.) If the test is reliable it should rank order the individuals in essentially the same way on both occasions. If one person obtains a score that places him in the 75th percentile of a given population one week and in the 25th percentile the next week, one would be rightly suspicious of the test’s reliability.
A major factor affecting test reliability is the length of the assessment. An assessment with ten items or exercises will, other things being equal, be less reliable than one with 20 items or exercises. To see why this is so, consider the following thought experiment. Suppose we arranged a golf match between a typical weekend golfer and the phenomenal Tiger Woods. The match (read “test”) will consist of a single, par-3 hole at a suitable golf course. Although unlikely, it is entirely conceivable that the weekend golfer could win this “one item” contest. He or she could get lucky and birdie the hole, or if they are really lucky, get a hole in one. Mr. Woods might well simply par the hole, as he has done countless times in his career. Now suppose that the match consisted not of one hole, but of an entire round of 18 holes. The odds against the weekend golfer winning this longer, more reliable match are enormous. Being lucky once or twice is entirely credible, but being lucky enough to beat Mr. Woods over the entire round taxes credulity. The longer the “test,” the more reliably it reflects the two golfers’ relative ability.
Newcomers to testing theory often confuse validity and reliability; some even use the terms interchangeably. A brief, exaggerated example will illustrate the difference between these two essential testing concepts. We noted above that a reliable test rank orders individuals in essentially the same way on two separate administrations of the test. Now, let us suppose that one were to accept, foolishly, the length of a person’s right index finger as a measure of their vocabulary. To exclude the confounding effects of age, we will restrict our target population to persons 18 years of age and older. This is obviously a hopelessly invalid measure of the construct “vocabulary.” But note that were we to administer our “vocabulary” test on two separate occasions (that is, were we to measure the length of the index fingers of a suitable sample of adults on two separate occasions), the resulting two rank orderings would be virtually identical. We have a highly reliable but utterly invalid test.
The numerical index of reliability is scaled from 0, the total absence of reliability, to 1, perfect reliability. What does zero reliability mean? Consider another thought experiment. Many people believe that there are individuals who are naturally luckier than the rest of us. Suppose we were to test this notion by attempting to rank order people according to their “coin tossing ability.” Our hypothesis is that when instructed to “toss heads,” some individuals can do so consistently more often then others. We instruct 50 randomly chosen individuals to toss a coin 100 times. They are to “attempt to toss as many heads as possible.” We record the number of heads tossed by each individual. The experiment is then repeated and the results are again recorded. It should come as no surprise that the correlation between the first rank order and the second would likely be near zero. The coin-tossing test has essentially zero reliability.
Perfect reliability, on the other hand, implies that both the rank orders and score distributions of a large sample of persons on two administrations of the same test, or on the administrations of equivalent tests, would be identical. The finger test of vocabulary discussed above is an example. In educational and psychological assessment, perfect reliability is hard to come by.
Fires and Eternity
October 25, 2007
Education is not the filling of a pail, but the lighting of a fire.
—William Butler Yeats
In a Carnegie Perspectives essay, I argued that one way for teachers to gauge their effectiveness is to ask the same carefully crafted questions before and after instruction. The essay sparked a lively debate over what constitutes a teacher’s effect on student learning. One educator, Thorpe Gordon, felt obliged to respond to the criticism that ascribing student learning to an individual teacher during the course of a semester or school year is problematic because students acquire relevant knowledge from many sources external to the class itself, including TV and the Internet. He had this to say:
Is not part of our job to encourage the love of learning and thus the lifelong learning of the topic to which we are presenting the students as their “first course” of a lifelong meal? While teaching environmental scanning in our topic area, I am very pleased if students use their own curiosity to discover other ways of learning and integrating the material, even if that includes the Discovery Channel. Thus, is that also not material that they did not know before the start of the course and the purpose of pre/post testing?
Gordon’s point is on the mark, and it would be unfortunate if readers interpreted my original essay as implying that a teacher’s influence and impact are limited to only that which transpired in the classroom. If the presentation of the subject matter is sufficiently engaging and students are inspired to learn more about the subject from a variety of other sources, well and good. If the class induces in students a heightened sensitivity to incidental information they encounter elsewhere, fine. This is precisely what teachers should strive for, and such learning can rightly be claimed as one of the effects of good instruction. But teacher effects go even beyond this.
When people are asked “Who had the most influence on your life and career?” countless polls and surveys have shown that teachers are second only to parents in the frequency with which they are mentioned. (Aristotle would have reversed the finding. “Those who educate children well,” he wrote, “are more to be honored than parents, for these only gave life, those the art of living well.”)
Two strikingly consistent features of these surveys are that, first, the teachers cited do not come from a single segment of the educational hierarchy, they span the spectrum from elementary school through high school to college and professional school. Second, student testimonials only occasionally center on what went on in class, or the particular knowledge they acquired. For the most part they talk about how the teacher affected their entire disposition toward learning and knowledge. Many even mention a complete shift in their choice of a career.
The U.S. Professor of the Year Program, sponsored jointly by the Carnegie Foundation and The Association of American Colleges and Universities (AACU), has illustrated the latter finding over and over again. The award is given annually to four professors, one each from a community college, a four-year baccalaureate college, a comprehensive university and a doctoral/research university. Nominations must be accompanied by statements of endorsement from colleagues, university administrators and students. (Thanks to Carnegie Senior Scholar Mary Huber, one of the two directors of the program, it has been my good fortune to read many of these statements over the past few years.) The statements from administrators and colleagues are uniformly glowing, but it is those from students that really grab one.
A community college student changed her entire career path (from accounting to writing and liberal arts) as a result of her study with one professor. A student at a doctoral/research university recounts how years after his graduate study his very thinking and approach to his discipline (physics) are still traceable to the mentorship under his major professor. In virtually every student recommendation, the students talked only briefly about what went on in the classroom. Rather, they stressed how their mentors affected their very disposition toward learning and life.
Our understanding of what constitutes good teaching has made enormous strides since the days of classroom observational protocols and behavioral checklists. We now know that a sound assessment of teaching must include, among other things, a thorough examination of teacher assignments, of the student products those assignments evoke, of the quality and usefulness of student feedback, and of how effectively teachers make subject matter content accessible to their students. It is also clear that however refined our assessments of teaching become, they inevitably will tell only part of the story. Henry Adams had it right, “Teachers affect eternity; they can never tell where their influence stops.”
Coaching and Test Validity
October 25, 2007
A continuing concern on the part of testing specialists, admissions officers, policy analysts and others is that commercial “coaching” schools for college and graduate school admissions tests, if they are effective in substantially raising students’ scores, could adversely affect the predictive value of such tests in college admissions. It is instructive to examine this concern in some detail.
The coaching debate goes to the heart of several fundamental psychometric questions. What is the nature of the abilities measured by scholastic aptitude tests? Are failures to substantially increase scores through coaching the result of failure in pedagogy or of the inherent difficulty of teaching thinking and reasoning skills? To what extent do score improvements that result from coaching contribute to or detract from test validity?
With respect to the possible adverse affects on predictive validity, three outcomes of coaching are possible. The 2 x 2 table below, a deliberately oversimplified depiction of how college and professional school admissions decisions are actually made, will serve to illustrate these three outcomes. The horizontal axis, representing admission test scores, has been dichotomized into scores below and above the “cut score” for admission. The vertical axis has been dichotomized into successful and unsuccessful performance in school. Applicants in the lower left quadrant and the upper right quadrant represent “correct” admissions decisions. Those in the lower left quadrant (valid rejections) did not achieve scores high enough to be accepted, and, had they been accepted anyway, they would have been unsuccessful. Students in the upper right hand quadrant (valid acceptances) exceeded the cut score on the test and successfully graduated. Applicants in the upper left and lower right quadrants represent incorrect admissions decisions. Those in the upper left quadrant (false rejections) did not achieve scores high enough to be accepted, but had they been accepted, they would have succeeded in college. Those in the lower right quadrant (false acceptances) were accepted in part on the basis of their test scores, but were unsuccessful in college.
One possible effect of coaching is that it might improve both the abilities measured by the tests and the scholastic abilities involved in doing well in college. For the borderline students, coaching in this case (arrow 1) would have the wholly laudatory effect of moving the student from the “valid rejection” category to the “valid acceptance” category. No one could reasonably argue against such an outcome.
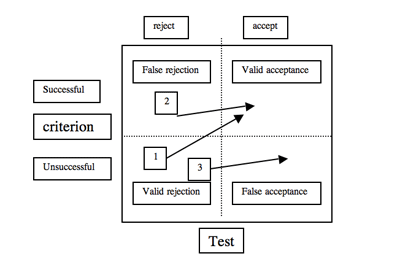
A second possible effect of coaching concerns the student who, because of extreme test anxiety or grossly inefficient test-taking strategies, obtains a score that is not indicative of his or her true academic ability. Coaching in the fundamentals of test taking, such as efficient time allocation and appropriate guessing, might cause the student to be more relaxed and thus improve his or her performance. The test will then be a more veridical reflection of ability. This second case might result in the student moving from the false rejection category to the valid acceptance category (arrow 2) and again this is an unarguably positive outcome.
The third possible outcome of coaching is not so clearly salutary. The coached student moves from the valid rejection category to the false acceptance category (arrow 3). The coached student increases his or her performance on the test, but there is no corresponding increase in the student’s ability to get good grades. Case three is an example of what the late David McClelland derisively called “faking high aptitude.”
Actual research on the extent to which these outcomes occurs is conspicuous by its absence. If the first two results dominate, that simply adds to the validity of the test. If the third turns out to be widespread, then it implies not so much deficiencies in our understanding of scholastic aptitude as serious deficiencies in tests designed to measure that aptitude. In any event, more research is needed on precisely such issues. One way to better understand a phenomenon is to attempt to change it. In so doing, we may come to better understand the nature of expert performance, the optimal conditions under which it progresses, and the instructional environments that foster its development.
In 1989, in a more in-depth treatment of the coaching debate, I concluded with the following statement. I believe it applies with equal force today:
The coaching debate will probably continue unabated for some time to come. One reason for this, of course, is that so long as tests are used in college admissions decisions, students will continue to seek a competitive advantage in gaining admission to the college of their choice. A second more scientifically relevant reason is that recent advances in cognitive psychology have provided some hope in explicating the precise nature of aptitude, how it develops, and how it can be enhanced. This line of research was inspired in part by the controversy surrounding the concepts of aptitude and intelligence and the felt inadequacy of our understanding of both. Green (1981) noted that social and political challenges to a discipline have a way of invigorating it, so that the discipline is likely to prosper. So it is with the coaching debate. Our understanding of human intellectual abilities, as well as out attempts to measure them, is likely to profit from what is both a scientific and a social debate.
Reference
Green, B. F. (1981). A primer of testing. American Psychologist. 10, 1001-1011.
McClelland, D. (1973). Testing for competence rather than intelligence. American Psychologist.
The Think-Aloud Protocol: A High Yield/Low Stakes Assessment
October 25, 2007
A verbal or “think-aloud” protocol is a transcribed record of a person’s verbalizations of her thinking while attempting to solve a problem or perform a task. In their classic book, Verbal Reports as Data, Ericcson & Simon liken the verbal protocol to observing a dolphin at sea. Because he occasionally goes under water, we see the dolphin only intermittently, not continuously. We must therefore infer his entire path from those times we do see him. A student’s verbalizations during problem solving are surface accounts of her thinking. There are no doubt “under water” periods that we cannot observe and record; but with experience, the analysis of students’ verbalizations while trying to perform a task or solve a problem offers powerful insights into their thinking.
The following problem is an item from a retired form of the SAT-Math test:
If X is an odd number, what is the sum of the next two odd numbers greater than 3X + 1?
(a) 6X + 8
(b) 6X + 6
(c) 6X + 5
(d) 6X + 4
(e) 6X + 3
Less than half of SAT test takers answered this item correctly, and the actual percentage is no doubt smaller since some students guessed the correct alternative. To solve the problem the student must reason as follows:
If X is an odd number, 3X is also odd, and 3X + 1 must be even. The next odd number greater than 3X + 1 is therefore 3X + 2. The next odd number after that is 3X +4. The sum of these two numbers is 6X + 6, so the correct answer is option (b).
The only knowledge required to solve the problem is awareness of the difference between odd and even integers and the rules for simple algebraic addition. Any student who has had an introductory course in Algebra possesses this knowledge, yet more than half could not solve the problem.
Test development companies have data on thousands of such problems from many thousands of students. But for each exercise, the data are restricted to a simple count of the number of students who chose each of the five alternatives. Such data can tell us precious little about how students go about solving such problems or the many misconceptions they carry around in their heads about a given problem’s essential structure. Perhaps more than any other tool in an instructor’s armamentarium, the think-aloud protocol is the prototypical high yield/low stakes assessment.
In a series of studies I conducted some time ago at the University of Pittsburgh, I was interested in why so many students perform well in high school algebra and geometry, but poorly on the SAT-Math test. The performance pattern of high grades/low test scores is an extremely popular one, and the reasons underlying the pattern are many and varied. The 28 students that I studied allowed me to record their verbalizations as they attempted to solve selected math items taken from retired forms of the SAT. All of the students had obtained at least a “B” in both Algebra I and Geometry. Here is the protocol of one student (we will call him R) attempting to solve the above problem. In the transcription, S and E represent the student and the experimenter, respectively.
1. S: If X is an odd number, what is the sum of the next two odd numbers greater than 3X plus 1?
2. (silence)
3. E: What are you thinking about?
4. S: Well, I’m trying to reason out this problem. Uh, ok I was. . . If X is an odd number, what is the sum of the next two odd numbers greater than 3X plus one? So. . . I don’t know, lets see.
5. (long silence)
6. S: I need some help here.
7. E: Ok, hint: If X is an odd number, is 3X even or odd?
8. S: Odd.
9. E: OK. Is 3X plus 1 even or odd?
10. S: Even.
11. E: Now, does that help you?
12. S: Yeah. (long silence)
13. E: Repeat what you know.
14. S: Uh, lets see . . . uh, 3X is odd, 3X plus 1 is . . . even.
15. (long silence)
16. E: What is the next odd number greater than 3X plus 1?
17. S: Three? Put in three for X . . . and add it. So it would be 10?
18. E: Well, we’ve established that 3X plus 1 is even, right?
19. S: Yeah.
20. E: Now, what is the next odd number greater than that?
21. S: Five?
22. E: Well, X can be ANY odd number, 7 say. So if 3X plus 1 is even, what is the next odd number greater than 3X plus 1?
23. S: I don’t know.
24. E: How about 3X plus 2?
25. S: Oh, oh. Aw, man.
26. (mutual laughter)
27. S: I was trying to figure out this 3X . . . I see it now.
28. E: So what’s the next odd number after 3X plus 2?
29. S: 3X plus 3.
30. E: The next ODD number.
31. S: Next ODD number? Oh, oh. You skip that number . . . 3X plus 4. So let’s see…
32. (long silence)
33. E: Read the question.
34. S: (inaudible) Oh, you add. Let’s . . . It’s b. It’s 6X plus 6. Aw, man.
Two points are readily apparent from this protocol. The first is that R could not generate on his own a goal structure for the problem. Yet, when prompted, he provided the correct answers to all relevant subproblems. Second, R does not appear to apprehend the very structure of the problem. This is so despite the fact that the generic character of the correct answer (that is, in the expression 6X + 6, X may be any odd number) can be deduced from the answer set. R tended to represent the problem internally as a problem with a specific rather and a general solution. Hence, in responding (line 13) to my query with a specific number (i.e., 10), he was apparently substituting the specific odd number 3 into the equation 3X + 1. (Even here the student misunderstood the question and simply gave the next integer after 3X, rather than responding with 11, the correct specific answer to the question. This was obviously a simple misunderstanding that was later corrected.) The tendency to respond to the queries with specific numeric answers rather than an algebraic expression in terms of X was common. A sizable plurality of the 28 students gave specific, numeric answers to this same query.
This protocol is also typical in its overall structure. Students were generally unable to generate on their own the series of sub-goals that lead to a correct solution. But they experienced little difficulty in responding correctly to each question posed by the experimenter. The inability to generate an appropriate plan of action and system of sub-goals, coupled with the ability to answer correctly all sub-questions necessary for the correct solution, characterize the majority of protocols for these students.
Compare the above with the following protocol of one of only two students in the sample who obtained “A’s” in both Algebra and Geometry and who scored above 600 on the SAT-Math. The protocols for the above problem produced by these two students were virtually identical.
(Reads question; rereads question)
S: Lets see. If X is odd, then 3X must be . . . odd. And plus 1 must be even. Is that right? Yeah . . . So . . . what is the sum of the next two odd . . . so that’s . . . 3X plus 2 and . . . 3X plus . . . 4. So . . . you add. It’s b, it’s 6X plus 6. (Total time: 52 seconds)
As a general rule, problems like the one above (that is, problems that require relevant, organized knowledge in long-term memory and a set of readily available routines that can be quickly searched during problem solving) presented extreme difficulties for the majority of the students. For many of these students, subproblems requiring simple arithmetic and algebraic routines such as the manipulation of fractions and exponents represented major, time-consuming digressions. In the vernacular of cognitive psychologists, the procedures were never routinized or “automated.” The net effect was that much solution time and in fact much of the students’ working memory were consumed in solving routine intermediate problems, so much so that they often lost track of where they were in the problem.
A careful analysis of these protocols, coupled with observations of algebra classes in the school these students attended, led me to conclude that their difficulties were traceable to how knowledge was initially acquired and stored in long-term memory. The knowledge they acquired about algebra and geometry was largely inert, and was stored in memory as an unconnected and unintegrated list of facts that were largely unavailable during problem solving.
The above insights into student thinking could not have been made from an examination of responses to multiple-choice questions, nor even from responses to open-ended questions where the student is required to “show your work.” For, as any teacher will attest, such instructions often elicit unconnected and undecipherable scribbles that are impossible to follow.
For instructors who have never attempted this powerful assessment technique, the initial foray into verbal protocol analysis may be labor intensive and time-consuming. For students, verbalizing their thoughts during problem solving will be distracting at first, but after several practice problems they quickly catch on and the verbalizations come naturally with fewer and fewer extended silences.
In many circumstances, the verbal protocol may well be the only reliable road into a student’s thinking. It is unquestionably a high yield, low stakes road. I invite teachers to take the drive. They will almost certainly encounter bumps along the way, and a detour or two. But the scenery will intrigue and surprise. Occasionally it will even delight and inspire.